Trapezium Basics
What is a Trapezium?
Trapezium is a quadrilateral with one pair of parallel sides.
In the above figure, AB ∥ CD
That is, AB ∥ CD and BC = AD
A parallelogram is a trapezium. However, vice-versa need not be true, i.e. a trapezium need not be a parallelogram - as only one pair of opposite sides is parallel in a trapezium and we require both pairs to be parallel in a parallelogram.
Properties of Trapezium
These are the properties that are true for any kind of trapezium.
Property 1: Angles
Consecutive angles along both non-parallel sides are supplementary, i.e. their sum is equal to 180°.
That is, if AB ∥ CD then:
∠A + ∠D = 180°, and
∠B + ∠C = 180°
Sum of interior angles (or exterior angles) on the same side of the transversal line is supplementary.
In case of Isosceles trapeziums, consecutive angles along each parallel sides are equal too.
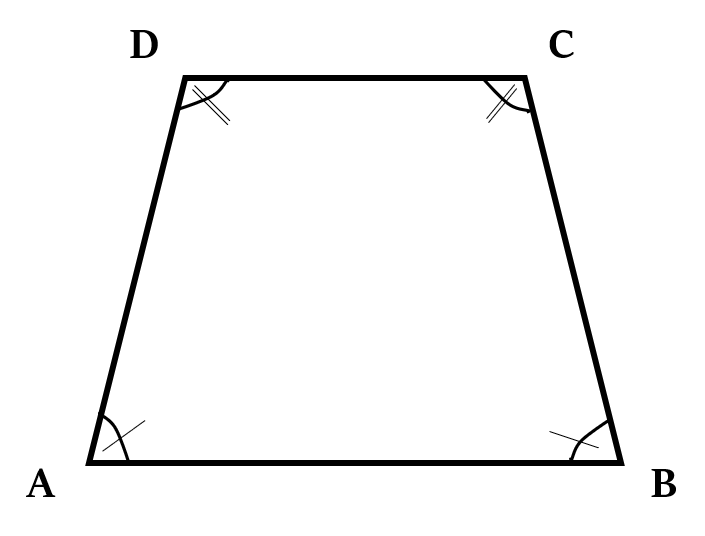
That is, if AB ∥ CD and BC = AD, then:
∠A = ∠B, and
∠C = ∠D
Property 2: Diagonals
Diagonals of a trapezium intersect each other proportionally.
$\frac{AO}{OC}$ = $\frac{BO}{OD}$
In case of Isosceles trapeziums, diagonals are equal too.
That is, if AB ∥ CD and BC = AD, then:
AC = BD
Property 3: A line parallel to the parallel sides
Any line parallel to the parallel sides of a trapezium divides the non-parallel sides proportionally.
In the above figure, if AB ∥ PQ ∥ DC then,
$\frac{AP}{PD}$ = $\frac{BQ}{QC}$
Mid-point Theorem: A Special Case
If the line parallel to the parallel sides of a trapezium, passes through the mid points of non-parallel sides, then its length will be equal to half of the sum of parallel sides.
In the above figure, if $\frac{AP}{PD}$ = $\frac{BQ}{QC}$ = 1, i.e. AP = PD and BQ = QC, then:
PQ = $\frac{AB + DC}{2}$