Quadrilateral Basics
What is a Quadrilateral?
Quadrilateral is a two-dimensional enclosed figure formed by joining four points on a plane.

So, a quadrilateral has four vertices and four sides.
Some examples of quadrilaterals are: Parallelogram, Trapezium, Kite etc.
Types of Quadrilaterals
Parallelogram
It is a quadrilateral with two pairs of parallel sides.
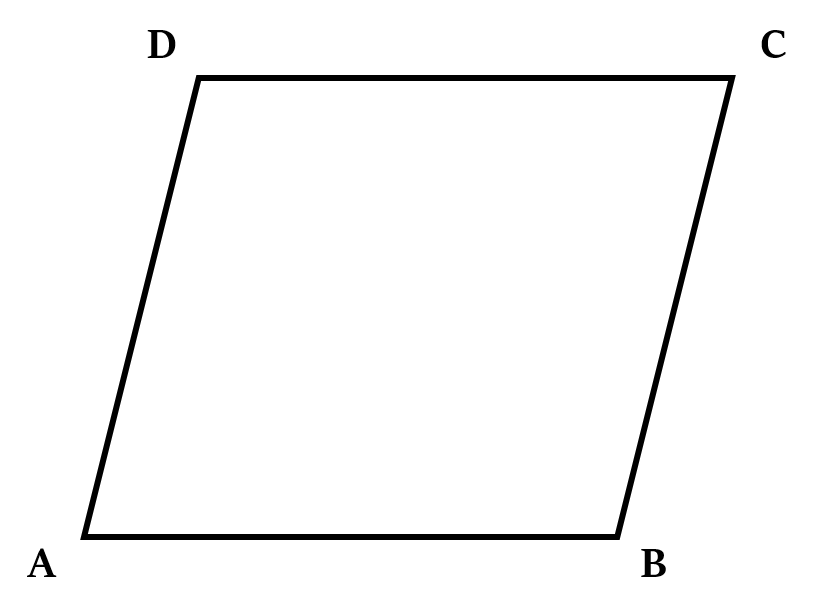
- The opposite sides of a parallelogram are parallel and are of equal length.
- The opposite angles of a parallelogram are also equal. That is, ∠ A = ∠ C; ∠ B = ∠ D
There are various kinds of parallelograms, such as Rhombus, Rectangle, Square. We will study about these in much more detail in a separate article.
Trapezium
It is a quadrilateral with one pair of parallel sides.
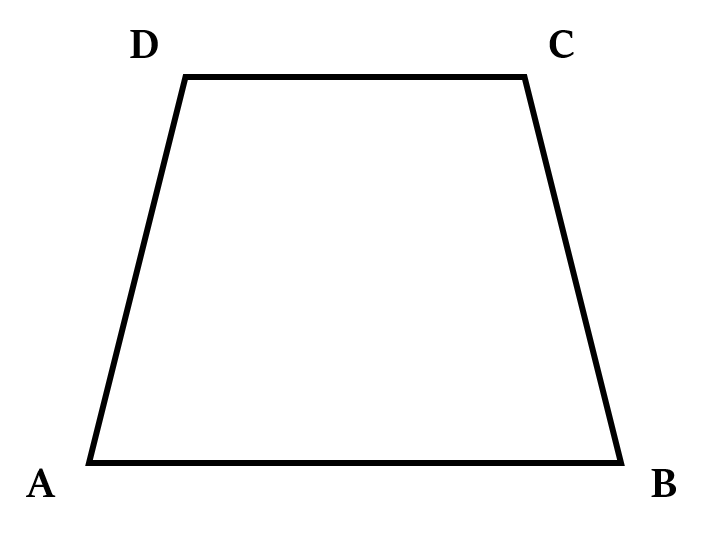
In the above figure, AB ∥ CD
That is, AB ∥ CD and BC = AD
Kite
It is a quadrilateral in which two pairs of adjacent sides are equal.

In the above figure, AB = AD, and CB = CD
A Kite is not a parallelogram.
Square and Rhombus are both Parallelogram and Kite.
Cyclic Quadrilateral
Cyclic Quadrilateral is a kind of quadrilateral, all of whose vertices lie on the circumference of a circle.

Circumscribed Quadrilateral
Circumscribed Quadrilateral is a convex quadrilateral, all of whose four sides are tangent to a single circle within it. That’s why it’s also called Tangential Quadrilateral.

Properties of Quadrilaterals
Let’s see some of the properties shared by all types of quadrilaterals.
Property 1: Angle Sum
Sum of the four interior angles of a quadrilateral is 360°.
 In the above quadrilateral, ∠ A + ∠ B + ∠ C + ∠ D = 360°
In the above quadrilateral, ∠ A + ∠ B + ∠ C + ∠ D = 360°
Similarly, Sum of the four exterior angles of a quadrilateral is also 360°.
Property 2
If we join the mid-points of the four sides of a quadrilateral, then we will get a parallelogram. The area of this parallelogram will be half of the original quadrilateral.

In the above figure, on joining the mid-points of the sides of the quadrilateral □ABCD, we get a parallelogram PQRS.
Area of parallelogram PQRS =
If we join the mid-points of the four sides of a parallelogram, then we will get a parallelogram. The area of this parallelogram will be half of the original parallelogram.
This is obvious, as a parallelogram is also a quadrilateral.
Property 3
Angle made by the bisectors of any two consecutive angles = Half of the sum of the other two angles

In the above figure, ∠AOB =
Property 4
Sum of a pair of interior opposite angles = Sum of the pair of other two exterior opposite angles

In the above figure, ∠x° + ∠y° = ∠p° + ∠q°
Property 5
The line segment joining midpoints of any two adjacent sides is parallel and equal to half of corresponding diagonal.

In the above figure, PQ ∥ AC and PQ =
Property 6
Perimeter of a quadrilateral is always greater than the sum of its diagonals.

In the above figure, AB + BC + CD + DA > AC + BD
Properties of Kites
Property 1: Diagonals
Diagonals of a Kite intersect at 90° and the shorter diagonal is bisected by the longer diagonal.

Properties of Cyclic Quadrilaterals
Property 1: Sum of Opposite angles
In any cyclic quadrilateral, the sum of either pair of opposite angles = 180°.

That is, ∠A + ∠C = 180°
And, ∠B + ∠D = 180°
Property 2
If the two diagonals of a cyclic quadrilateral ABCD intersect each other at a point P, then:

AP × PC = DP × PB
Property 3: In case of Square
Diagonal of inscribed square = Diameter of circle

Properties of Circumscribed Quadrilaterals
Property 1
Sum of opposite sides of a Circumscribed Quadrilateral are equal.

In the above figure, AB + CD = BC + AD
Property 2: In case of Square
Side of circumscribed square = Diameter of the inscribed circle
